Bau und Organisation einer Schulseismographenstation mit digitaler Fernabfrage und Konstruktion eines Lehrseismographen

3.2.4 Zur Lokalisation des Bebens

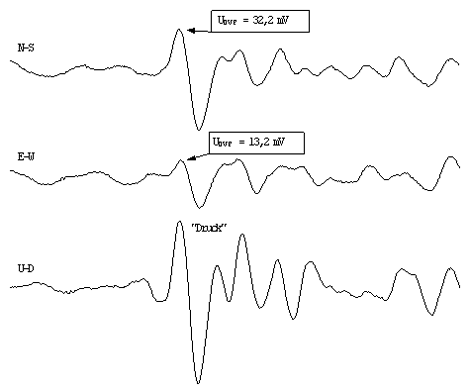
Zur Lokalisation des Bebens mittels einer Station benötigt man drei Seismographen (vgl. Abb. 3.2.4). Aus der Bodenamplitude des P-Wellen- Einsatzes von E-W- und N-S-Signal kann man nur die Richtung des Bebens bestimmen: die Apparatur kann nämlich nicht unterscheiden, ob die Welle z.B. eine Druckwelle aus Süd-West, oder eine Zugwelle nach Nord-Ost ist. Dies kann mit Hilfe des Vertikal-Seismographen entschieden werden.

Abb. 3.2.4: Vollständiges Seismogramm für die P-Einsätze des Ascension-Bebens vom 18.02.1996

Abb. 3.2.5: Zur Lokalisation des Erdbebens

Für das Ascension-Beben haben wir dann für den P-Wellen-Einsatz eine Bodenamplitude von a_0E(P)=1,927 µm in Ost-Richtung und in Nord-Richtung eine Bodenamplitude von a_0N(P)=5,756 µm. Der U-D-Seismograph signalisiert beim Ascension-Beben eine Druckwelle. Deswegen muss; der Richtungsvektor um 180° gedreht werden. Nun schließt der Richtungsvektor mit der Nord-Richtung den Winkel von α=161,5° ein. Diesen Richtungsvektor gleichen wir nun den Gauß-Krüger-Koordinaten an; da in unserem Fall beide Pendel im Keller nahezu senkrecht zueinander stehen (vgl. Abb. 2.2), müssen wir nur die Abweichung γ=8,4° (Außenwand Seismographenkeller zur Nord-Richtung) subtrahieren; also ergibt sich α_GK = 153,1°. Dieser Richtungsvektor liegt in der Tangential-Ebene an die Erdkugel am Stationsort und zeigt von dort in Richtung des Bebenherds (vgl. Abb. 3.2.5).

Bild zur Lokalisation des Ascension-Bebens vom 18.02.1996

Geometrisch bedeutet die Herd-Lokalisation die Bestimmung eines Kugeldreiecks aus zwei gegebenen Seiten (Poldistanz der Station Θ_s bzw. Herd-Entfernung Δ) und dem eingeschlossenen Winkel (Richtungswinkel α). Der Winkel, den die Poldistanzen Θ_s und Θ_H einschließen, soll Δλ heißen. Zur Ermittlung der Herd-Koordinaten (φ_H ; λ_H ) nutzt man zum einen aus, dass; der Richtungsvektor α senkrecht auf der Drehachse für die Drehung Station - Herd steht. Die Drehachse hat die Richtung des Vektorprodukts der Ortsvektoren von Station und Herd. Beachtet man auch, dass; Richtungsvektor und der Ortsvektor des Herds den Winkel 90°-Δ einschließen, dann findet man für die geographische Breite φ_H des Beben- Herds in Übereinstimmung mit dem Lehrbuch von Galitzin [11]:

φ_H = arcsin (cos Δ · sin φ_S + cos φ_s · cos α · sin Δ)

Zum anderen kann man über den Kosinus-Satz für das Dreieck Erdmittelpunkt M - Station S - Herd H die geographische Länge λ_H des Beben-Herds bestimmen:

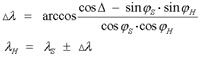
Das positive Vorzeichen wird für Ost-Richtung des Richtungsvektors α, das negative Vorzeichen für West-Richtung gewählt. Mit den Stationskoordinaten (φ_S ; λ_S ) = (50,554° ; 6,239°) von Monschau erhält man für die Herd-Koordinaten:

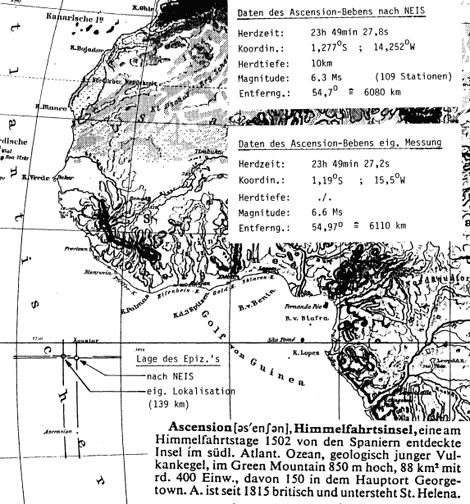
(φ_H ; λ_H ) = (1,19° S; 15,5° W) ,

die Herd-Koordinaten nach NEIS lauten:

(φ_H ; λ_H)NEIS = (1,28° S; 14,25° W) .

Nach unseren Berechnungen liegen wir 139 km neben dem tatsächlichen Epizentrum. Dies ist ein sehr gutes Ergebnis, da wir nur mit den Daten von unserer Station gerechnet haben, NEIS jedoch mit 109 Stationen.