2. On the seismogram as a "Journey through the interior of the earth"

Fig.19: Charles Richter (1900 - 1985)
who conceived the idea of the "Richter scale".

It is Charles Richter's merit to have invented a scale from which the strength of an earthquake can be calculated using instrumental measurements. For earthquakes that are recorded by a standardised seismograph (Wood-Anderson) having a maximum focus distance of 600 km Richter proposed his original scale. He used the largest displacement in the seismogram to calculate a value for the strength of an earthquake. (A different scale is the scale for earthquake-intensity, which is based on the destruction of buildings etc. caused by the earthquake.) - In correspondence to the astronomical scale for the brightness of stars Richter called the calculated value "magnitude". Later on seismologists extended Richter's scale to the recordings of earthquakes with larger focus distances.

The magnitude scale is a logarithmic scale, i.e. a quake with a magnitude of 6 has the tenfold amplitude as one with magnitude 5 and is one hundred times as strong as a quake with magnitude 4. For scientific seismology the Richter scale is nowadays no longer as important as in the past. Today press, broadcasting and TV use the scale mainly to classify an earthquake.

Let us now examine body waves.

Fig.20a: The propagation of earthquake waves in the earth: body waves

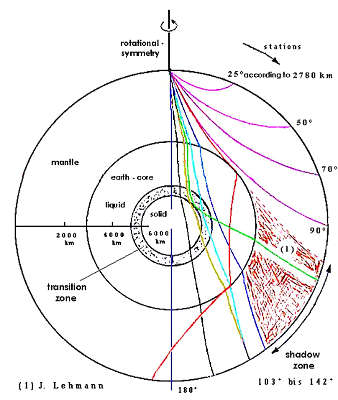
As one can see from the above graph, body waves do not propagate in a straight, but in a curved line within the earth. This can be explained in comparison with optics. The index of refraction decreases according to depth while the speed of propagation increases. (This is caused by the modules of elasticity for shear and compression increasing even faster than density with increasing depth).

Body waves that hit the outer liquid core of the earth are partly reflected and partly refracted into the liquid core where they then only exist as longitudinal waves. When the body waves exit the earth's core they are again broken and are partly converted to transverse waves.

One can clearly see in the graph that every earthquake has a so-called 'shadow-zone'. Quake waves can only reach this zone via complicated and manifold reflections. This is why seismological stations situated within this zone can only barely register the quake.

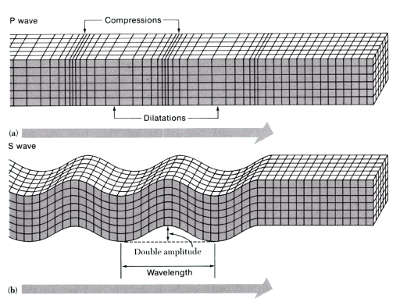
Also in body waves two wave types are distinguished, one of which is faster than the other.

Fig.20b: Body waves

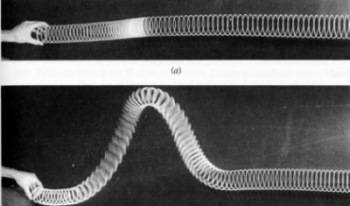
The faster wave is a longitudinal wave. How it propagates can easily be shown in a model made of coupled bar-pendulums, e.g. by suspended broomsticks, coupled with elastic bands. One begins by diverting a pendulum in the direction of propagation. But even a long 'soft' helical spring ('Slinky') can demonstrate this (see fig. 21b, upper panel).

Fig.21: Model for propagation of S- and P- waves

As the faster wave logically reaches the station first the longitudinal body wave is named primary wave or for short P-wave. The slower wave is called secondary wave, in contrast to the P-wave it has transverse propagation. This type of propagation is demonstrated in the broomstick model if one initially deflects the first pendulum transversely to the direction of propagation. Analogously the deflection of the 'Slinky' spring takes place (fig. 21b, lower panel).