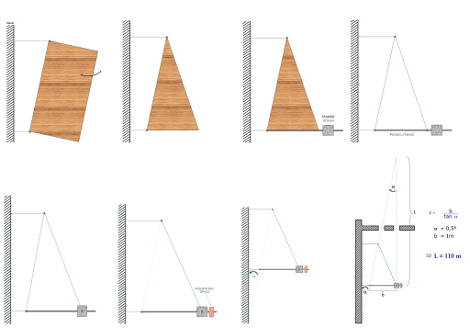
4.1 From the 'garden gate principle' to the horizontal seismograph

Our seismograph is a horizontal pendulum, which oscillates similarly to a garden gate; one often speaks of the 'garden gate principle'. A garden gate should not always remain open, but falls shut of its own accord. This is achieved by attaching the upper hinge somewhat further away from the upright post than the lower hinge. The time it takes for the door to fall shut depends on the angle between the hinges and the upright post. Is this angle of inclination small then the door closes slowly, if increased the door closes more quickly.

Before we describe details of our homemade seismograph, the following sketch shall explain why our horizontal seismograph contains the 'garden gate principle'.

The metamorphosis of a 'garden gate' pendulum

The first detail shows (if somewhat exaggerated to prove a point) a garden gate.

In the second stage the inner parts of the gate are 'removed' so that only a frame remains, of which the lower strut is horizontal. In the third stage this "boom" is lengthened to become a pendulum's rod on the end of which is placed a stone (with a central hole) as a pendulum weight. The part of the garden gate extending from the upper hinge is replaced by a wire, the ends of which are attached to either side of the weight at the height of the pendulum's boom. In the last stage we can now attach the induction coil to the boom and remove the part of the frame that connects the hinges.

If one describes the length of the pendulum's rod as b (the distance between the lower hinge point and the centre of the pendulum weight) then one can calculate the pendulum's period with the aid of the acceleration of the earth g and the angle of incline a as follows:

The size L* = b / tan a is the 'equivalent pendulum length' of a string pendulum with the same period T of oscillation as the garden gate pendulum: as one can see one finds L* by erecting an upright perpendicular to the (horizontally mounted) pendulum weight and consequently make it create a section with the straight line that runs through both hinge points.

With a pendulum length of one meter and an angle of incline of 0.5� (which is easily adjusted in our pendulum) there results the pendulum length of L* ≈ 115m..